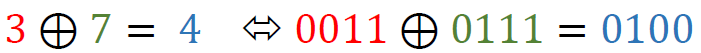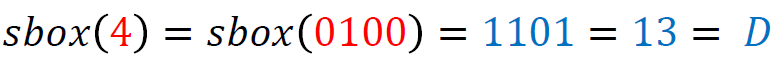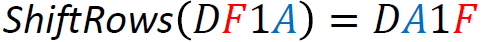In my journey through the world of cryptography, I’ve previously explored and shared insights on the Advanced Encryption Standard (AES) and the Data Encryption Standard (DES) — ciphers that hold a prominent place in Western cryptographic practices. Venturing further, I delved into the realm of Soviet/Russian cryptography with a detailed examination of the GOST Magma cipher in a YouTube video. Continuing on this path, I’ve now expanded my exploration to include the Chinese block cipher ShāngMì 4 (SM4 ,商密4). In the latest video on my YouTube channel (which you’ll find at the conclusion of this blog post), I explain the structure and mechanics of SM4, showcasing its unbalanced Feistel network design and its building blocks.
A look at SM4’s history
Originally named SMS4, the SM4 Block Cipher is not just an algorithm; it’s a testament to China’s stride towards self-reliance in information security. Drafted by the Data Assurance & Communication Security Center alongside the Commercial Cryptography Testing Center under the National Cryptography Administration, SM4 was officially released on March 21st, 2012. It transitioned from an internal specification to a national standard in China in August 2016. It is mainly developed by Lü Shuwang (Chinese: 吕述望).
SM4 overview
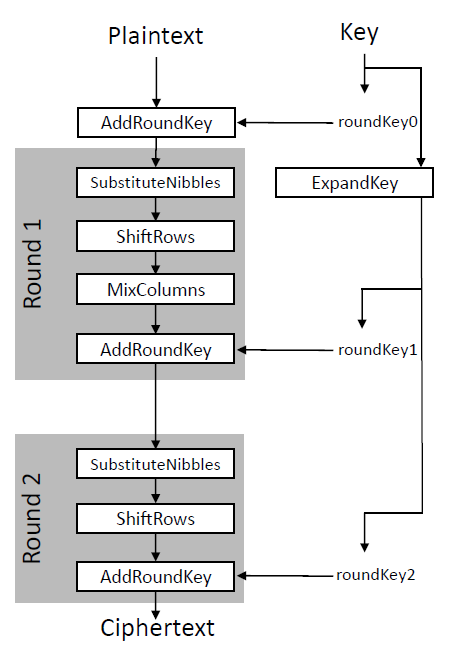
At its core, SM4 is a symmetric block cipher, characterized by a 128-bit block and key size, operating over 32 rounds. It employs an unbalanced Feistel network structure, utilizing an S-box for its non-linear transformation. Each round of the cipher involves linear and non-linear operations, including XORs, shifts, and table lookups within a so-called F function. Each round, a different of the 32 round keys is used.
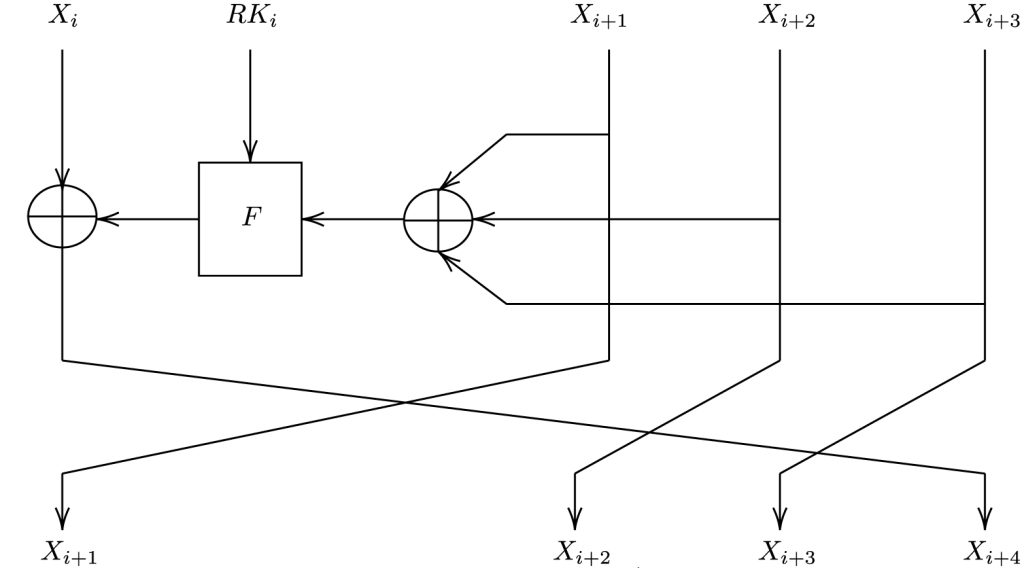
SM4 divides its 128-bit input into four 4-byte blocks (X0, X1, X2, and X3). The first block is XOR-ed with the result of the F function and becomes the new 4th block. The old second, third, and fourth blog become the new first, second, and third block.
The round function is the heart of SM4: the F function
The round function of SM4, denoted as F, is where the “magic happens”. It takes in four inputs along with a round key and undergoes a series of transformations, including XOR operations and the application of the T function. The T function itself is a blend of non-linear (Tau) and linear (L) transformations, ensuring that the output is highly unpredictable, thereby enhancing security.
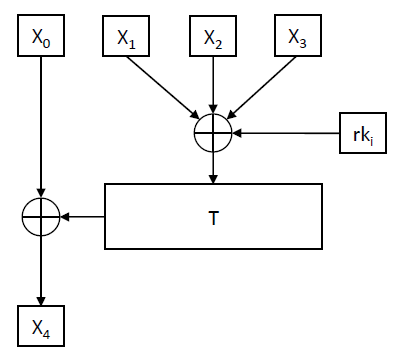
The f Function calls the T function, which calls the L function, which calls the Tau function (S-Box lookups):
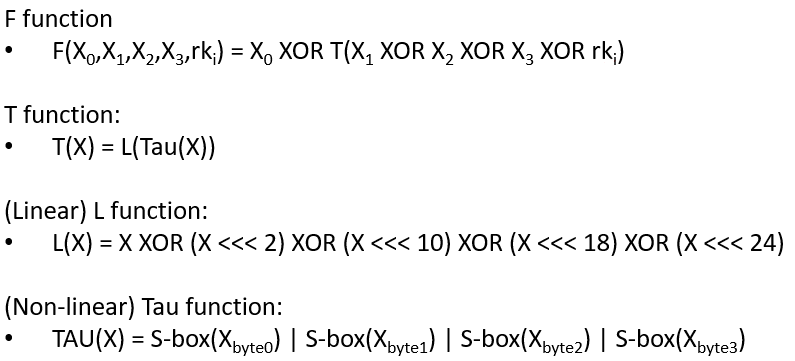
Below, we explain the non-linear function Tau as well as the linear function L.
The non-linear part: the Tau function
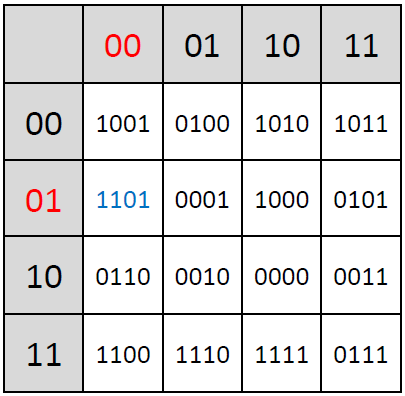
The non-linear function Tau, a fundamental component of the SM4 block cipher, plays a crucial role in the cipher’s security by introducing complexity and thwarting linear and differential cryptanalysis attacks. This function operates on the principle of substitution, where each byte of input is replaced with a corresponding byte from a pre-defined 8-bit S-box:
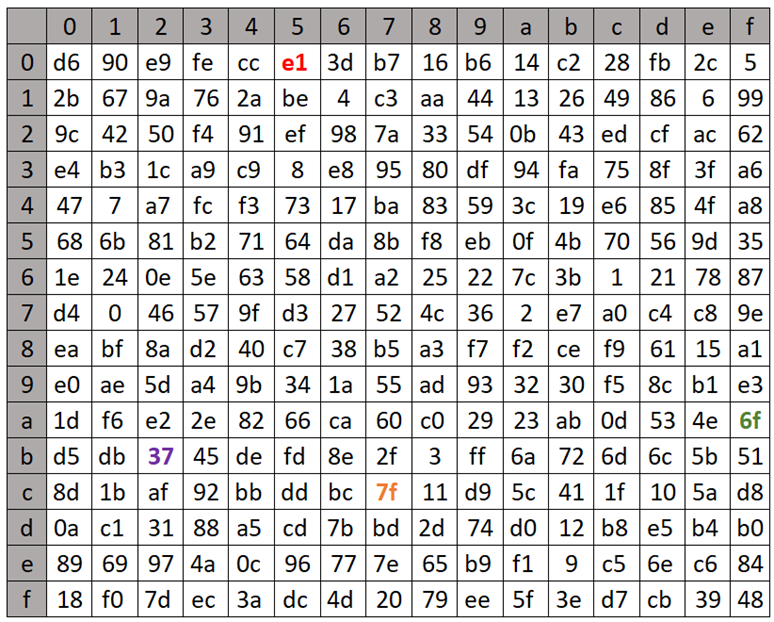
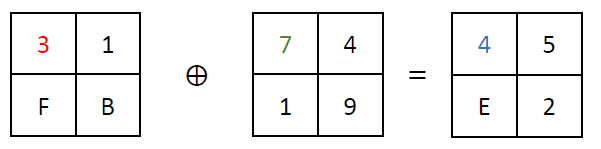
The Tau function processes input data in four bytes, applying the S-box transformation to each byte independently. The S-box, which stands for substitution box, is designed to be non-linear; it maps each 8-bit input to a new 8-bit output in a way that is deliberately non-linear and hard to predict. This unpredictability is what gives the Tau function its strength against cryptographic attacks, making the cipher more secure.
For example, given a 4-byte input, the Tau function applies the S-box transformation to each of these bytes. Example (values retrieved from the lookup table are highlighted in the same colors as used in the table depicted above; shown values are in hexadecimal format):

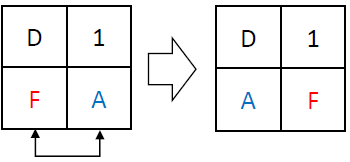
The linear part: the L function
The L function is a the second component of the F function, serving as the linear transformation stage that follows the non-linear Tau function in the encryption algorithm. Its primary role is to disperse the output of the Tau function across the block, enhancing the diffusion of the cipher. This process is essential for ensuring that changes in a single bit of the plaintext or the key propagate widely throughout the ciphertext, a property that strengthens the cipher against various forms of cryptanalysis.
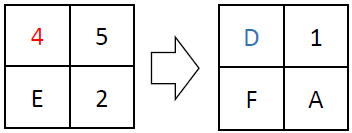
The L function operates by performing exclusive OR (XOR) operations on the input with shifted versions of itself. Specifically, it takes a 32-bit input and applies XOR with the input shifted left by 2, 10, 18, and 24 bits. This series of shifts and XORs ensures that the influence of each bit spreads across the entire block, contributing to the diffusion of the cipher. Its defined in the following equation; below is an example computation of the L function:

Decryption procedure
In the Feistel cipher design, the decryption process closely mirrors encryption, with a crucial difference: the round keys are applied in the opposite sequence. This means that during decryption, the keys are used in reverse order from how they were applied in encryption. This reversal is a key feature of the used Feistel structure, enabling the algorithm to easily reverse the encryption steps and recover the original plaintext.
The key expansion
The key expansion process in the SM4 block cipher is a systematic procedure designed to generate a series of round keys from the initial master key MK. The primary objective of the key expansion is to produce 32 round keys that are both unpredictable and resistant to cryptanalytic attacks.
At the beginning of the key expansion, the algorithm takes the master key MK, which is 128 bits in length, and processes it through a combination of XOR operations, non-linear transformations, and cyclic shifts to generate 32 round keys. The master key is initially divided into four words, and these words are then combined with predefined constants known as FK to produce the initial key state.
Following the initialization, the key expansion employs a loop that iterates 32 times to generate the 32 round keys. Each iteration of the loop applies a transformation function, denoted as T’, on a combination of the current key state and another set of constants called CK . The transformation function T’ is similar to the round function T but is adapted for the key expansion process. It includes the same S-box transformation (Tau) for non-linearity and a modified linear transformation (L’) that uses different cyclic shifts:

A paper about the cipher
A good paper on the cipher, written (and translated? from Chinese) by Whitfield Diffie and George Ledin, offering a comprehensive explanation, is available at the following link: https://eprint.iacr.org/2008/329
This paper also includes some of the design choices and explains how the S-box was created.
My YouTube video about the cipher
Of course, I also made a YouTube video for my “Cryptography for everbody” YouTube channel :-). You can watch it here: