ElsieFour (LC4)
Recently I stumbled across a very interesting cipher named ElsieFour (LC4), see specification in [1]. This cipher is a low tech cipher that can be computed by hand. It was developed by Alan Kaminsky and published in 2017. According to Kaminsky, it is designed hard to break. It is an amalgam of ideas from the RC4 stream cipher, the Playfair cipher, and the notion of plaintext dependent keystreams. It is a polyalphabetic substitution cipher. Besides encryption by hand, LC4 also allows authentication by hand. But this is not part of this blog article :-).
How does it work?
ElsieFour operates on a 36-letter plaintext alphabet A-Z, 0-9 (where 0 is # and 1 is _). The key is a permutation of this alphabet. LC4 uses a 6×6 grid filled with the keyed alphabet.
Encryption works as follows:
1. Choose a key (a particular permutation of the 36-character alphabet) and arrange it in a 6×6 grid
2. For each character in the plaintext message:
a) Determine the position of the character in the grid
b) Apply a sequence of movements in the grid (this includes moving the character, moving a “marker”, and possibly going around the edges of the grid) to determine the position of the ciphertext character
c) Write down the character at the new position as the next character in the ciphertext
d) Permute the grid in a specific way
Key Generation
Choose a key (a particular permutation of the 36-character alphabet) and arrange it in a 6×6 grid (e.g. “xv7ydq#opaj_39rzut8b45wcsgehmiknf26l”). And put the marker (red circle) into the top left corner. The tiles used for the grid are wooden plates which have the character and two small digits written on them:
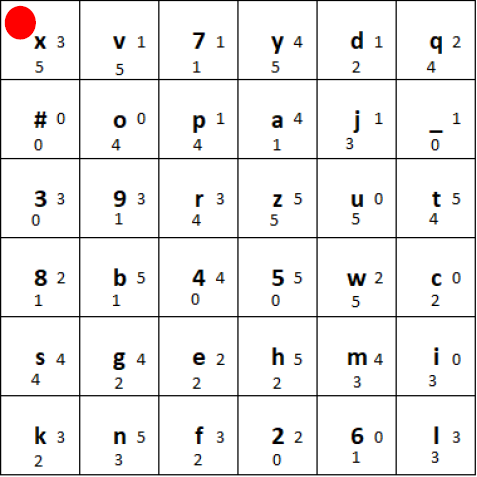
Initial state of the grid generated using the key
Encryption
Here, we encrypt for example the plaintext “hello world”. For each character in the plaintext message:
1) We determine the position of the character (here the letter “h”) in the grid:
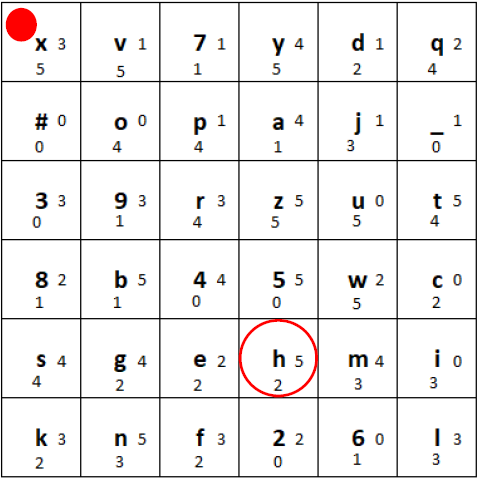
Marked position of the letter “h”
2) Then, we use the two small digits right and to the bottom of the marked letter. In this case the 3 and the 5. Go from the plaintext letter 3 to the right (wrapping around) and 5 to the bottom (wrapping around):
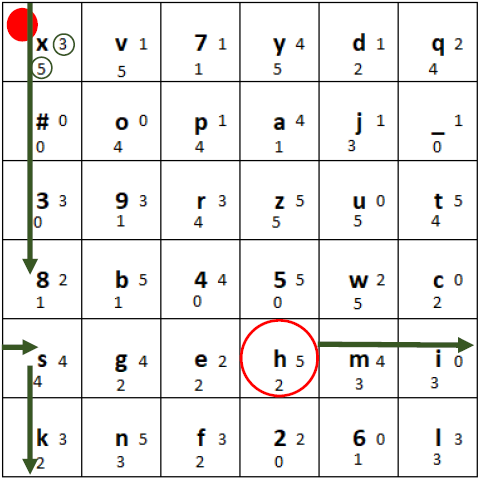
Determining the “movement” of the plaintext letter to obtain the ciphertext letter
3) After that, we write down the ciphertext letter (in this case the digit “8”).
4) Now, we permute the grid in the following way:
a) First, in the row with the plaintext character, we shift the tiles one position to the right, and put the rightmost tile at the beginning of the row:
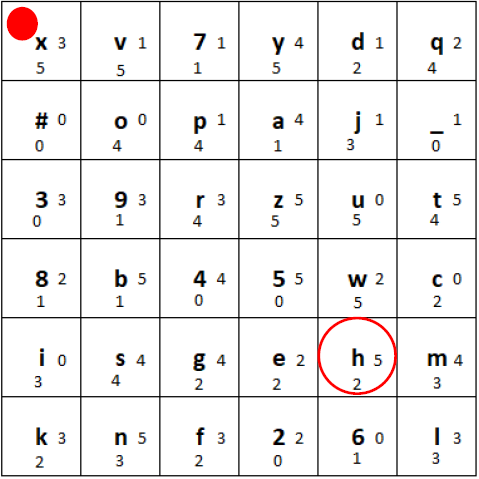
Plaintext row shifted one position to the right
b) Secondly, in the column with the ciphertext character, we shift the tiles one position down, and put the bottommost tile at the beginning of the column. If the marker’s tile moves, the marker stays on that tile:
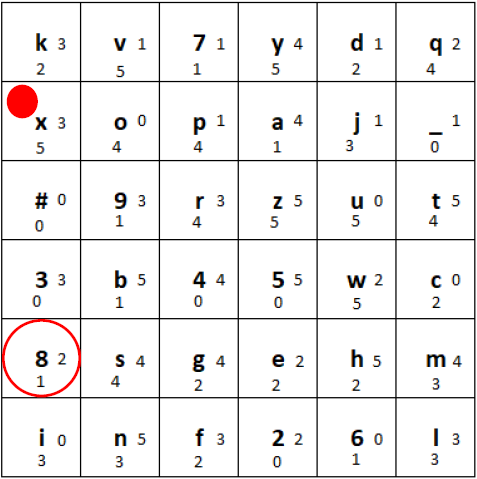
Ciphertext column shifted one position to the bottom.
c) Finally, we move the marker to the right the number of tiles shown at the right side of the ciphertext tile (here 2), wrapping around to the beginning of the row if necessary. We move the marker down the number of tiles shown at the bottom of the ciphertext tile (here 1), wrapping around to the beginning of the column if necessary.
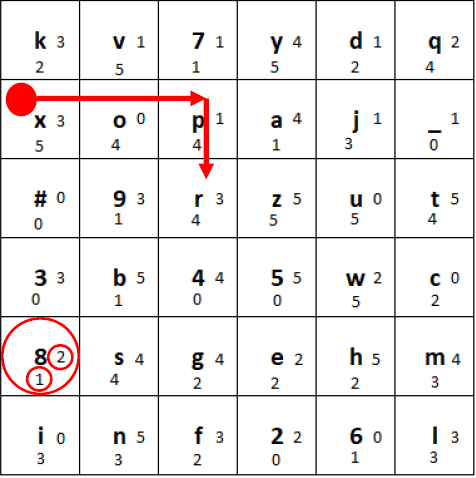
Moving of the marker
The final state of the grid after encrypting the first letter should look like this:
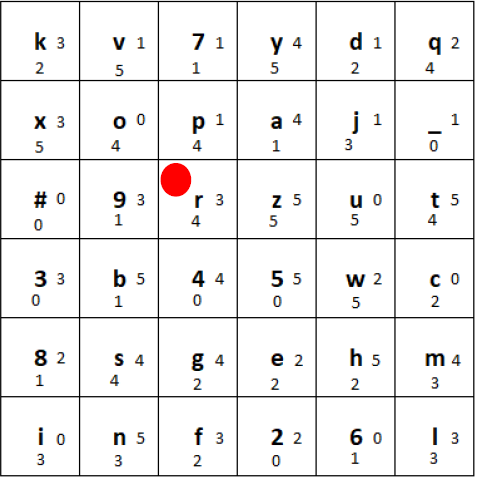
Final state after encrypting the first letter “h” and moving the tiles according to the rules
If we encrypt the plaintext “hello world” using the above shown procedure with every plaintext letter, the final ciphertext is “8#4l_3lcf8s”.
The decryption is the inverse process. We implemented the ElsieFour cipher in CrypTool 2, thus, if you want to use it without the need of creating wooden tiles, you can download CrypTool 2 and use the ElsieFour component :-). Go to https://www.cryptool.org/en/ct2/downloads
Keyspace size and unicity distance
The keyspace size k is the number of all possible permutations of the 36 letter alphabet:
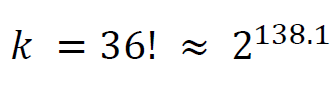
The unicity distance U is (entropy of keyspace H(k) divided by redundancy D of the language):
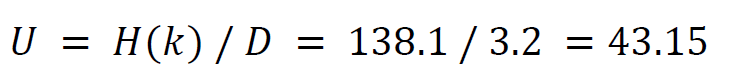
One final remark: If you make only one single mistake when encrypting or decrypting, the following plaintext or ciphertext is broken 🙁
A YouTube video about ElsieFour
I also made a YouTube video about the ElsieFour cipher :-). You can watch it here:
References
[1] Kaminsky, Alan. “ElsieFour: A Low-Tech Authenticated Encryption Algorithm For Human-To-Human Communication.” Cryptology ePrint Archive (2017). url: https://eprint.iacr.org/2017/339.pdf