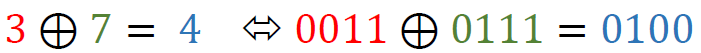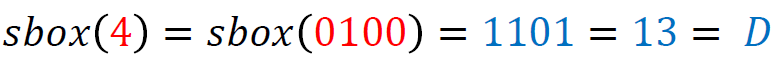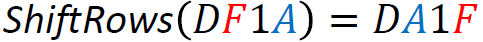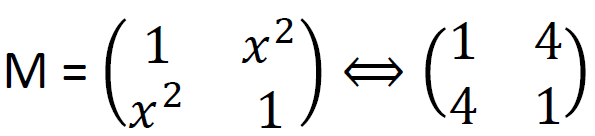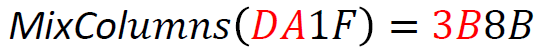Tag: modern

The ShāngMì 4 (SM4) Block Cipher: A Deeper Look into China’s Encryption Standard

Image of SM4 as an artistic representation

In my journey through the world of cryptography, I’ve previously explored and shared insights on the Advanced Encryption Standard (AES) and the Data Encryption Standard (DES) — ciphers that hold a prominent place in Western cryptographic practices. Venturing further, I delved into the realm of Soviet/Russian cryptography with a detailed examination of the GOST Magma cipher in a YouTube video. Continuing on this path, I’ve now expanded my exploration to include the Chinese block cipher ShāngMì 4 (SM4 ,商密4). In the latest video on my YouTube channel (which you’ll find at the conclusion of this blog post), I explain the structure and mechanics of SM4, showcasing its unbalanced Feistel network design and its building blocks.

A look at SM4’s history

Originally named SMS4, the SM4 Block Cipher is not just an algorithm; it’s a testament to China’s stride towards self-reliance in information security. Drafted by the Data Assurance & Communication Security Center alongside the Commercial Cryptography Testing Center under the National Cryptography Administration, SM4 was officially released on March 21st, 2012. It transitioned from an internal specification to a national standard in China in August 2016. It is mainly developed by Lü Shuwang (Chinese: 吕述望).

SM4 overview

At its core, SM4 is a symmetric block cipher, characterized by a 128-bit block and key size, operating over 32 rounds. It employs an unbalanced Feistel network structure, utilizing an S-box for its non-linear transformation. Each round of the cipher involves linear and non-linear operations, including XORs, shifts, and table lookups within a so-called F function. Each round, a different of the 32 round keys is used.

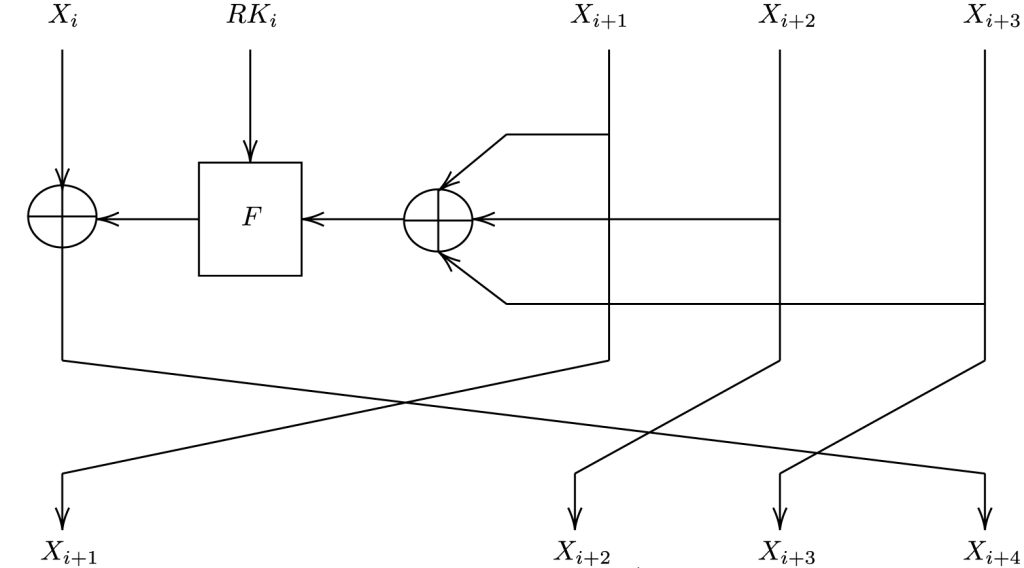
SM4 single round (image from Wikipedia)

SM4 divides its 128-bit input into four 4-byte blocks (X0, X1, X2, and X3). The first block is XOR-ed with the result of the F function and becomes the new 4th block. The old second, third, and fourth blog become the new first, second, and third block.

The round function is the heart of SM4: the F function

The round function of SM4, denoted as F, is where the “magic happens”. It takes in four inputs along with a round key and undergoes a series of transformations, including XOR operations and the application of the T function. The T function itself is a blend of non-linear (Tau) and linear (L) transformations, ensuring that the output is highly unpredictable, thereby enhancing security.

SM4 F function

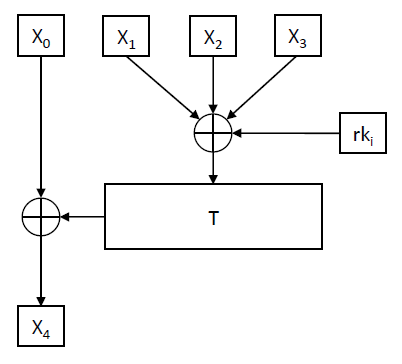
The f Function calls the T function, which calls the L function, which calls the Tau function (S-Box lookups):

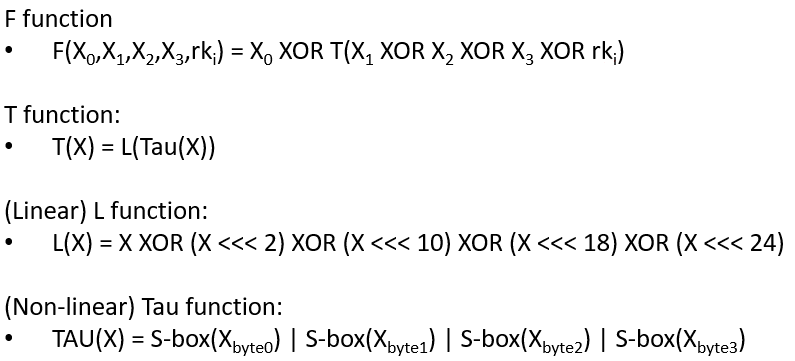
Equations of the F function (including T function, L function, and Tau function)

Below, we explain the non-linear function Tau as well as the linear function L.

The non-linear part: the Tau function

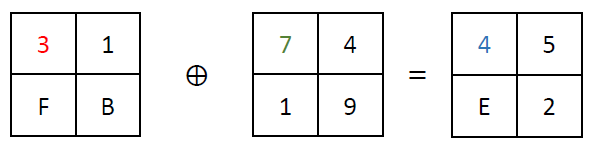
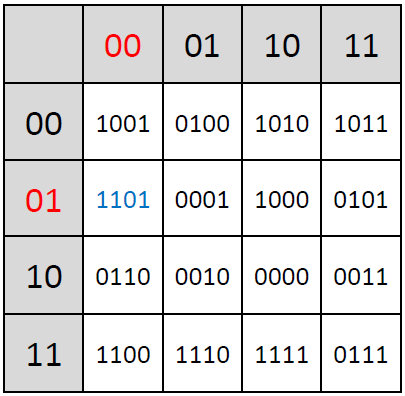
The non-linear function Tau, a fundamental component of the SM4 block cipher, plays a crucial role in the cipher’s security by introducing complexity and thwarting linear and differential cryptanalysis attacks. This function operates on the principle of substitution, where each byte of input is replaced with a corresponding byte from a pre-defined 8-bit S-box:

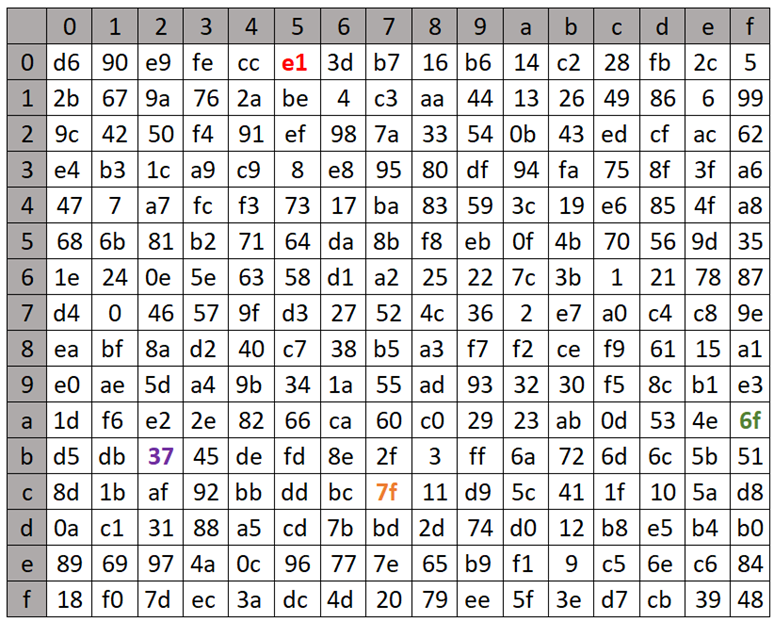
SM4 S-box (lookup table with 256 entries)

The Tau function processes input data in four bytes, applying the S-box transformation to each byte independently. The S-box, which stands for substitution box, is designed to be non-linear; it maps each 8-bit input to a new 8-bit output in a way that is deliberately non-linear and hard to predict. This unpredictability is what gives the Tau function its strength against cryptographic attacks, making the cipher more secure.

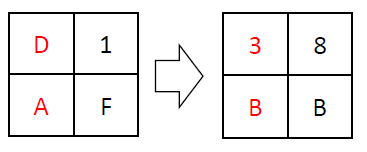
For example, given a 4-byte input, the Tau function applies the S-box transformation to each of these bytes. Example (values retrieved from the lookup table are highlighted in the same colors as used in the table depicted above; shown values are in hexadecimal format):

SM4 Tau function example computation

The linear part: the L function

The L function is a the second component of the F function, serving as the linear transformation stage that follows the non-linear Tau function in the encryption algorithm. Its primary role is to disperse the output of the Tau function across the block, enhancing the diffusion of the cipher. This process is essential for ensuring that changes in a single bit of the plaintext or the key propagate widely throughout the ciphertext, a property that strengthens the cipher against various forms of cryptanalysis.

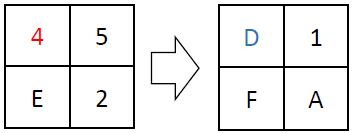
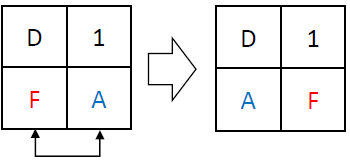
The L function operates by performing exclusive OR (XOR) operations on the input with shifted versions of itself. Specifically, it takes a 32-bit input and applies XOR with the input shifted left by 2, 10, 18, and 24 bits. This series of shifts and XORs ensures that the influence of each bit spreads across the entire block, contributing to the diffusion of the cipher. Its defined in the following equation; below is an example computation of the L function:

L function and example computation

Decryption procedure

In the Feistel cipher design, the decryption process closely mirrors encryption, with a crucial difference: the round keys are applied in the opposite sequence. This means that during decryption, the keys are used in reverse order from how they were applied in encryption. This reversal is a key feature of the used Feistel structure, enabling the algorithm to easily reverse the encryption steps and recover the original plaintext.

The key expansion

The key expansion process in the SM4 block cipher is a systematic procedure designed to generate a series of round keys from the initial master key MK. The primary objective of the key expansion is to produce 32 round keys that are both unpredictable and resistant to cryptanalytic attacks.

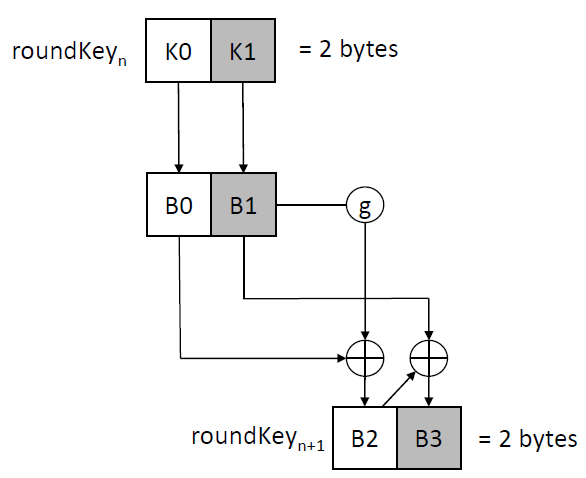
At the beginning of the key expansion, the algorithm takes the master key MK, which is 128 bits in length, and processes it through a combination of XOR operations, non-linear transformations, and cyclic shifts to generate 32 round keys. The master key is initially divided into four words, and these words are then combined with predefined constants known as FK to produce the initial key state.

Following the initialization, the key expansion employs a loop that iterates 32 times to generate the 32 round keys. Each iteration of the loop applies a transformation function, denoted as T’, on a combination of the current key state and another set of constants called CK . The transformation function T’ is similar to the round function T but is adapted for the key expansion process. It includes the same S-box transformation (Tau) for non-linearity and a modified linear transformation (L’) that uses different cyclic shifts:

Key expansion (equations)

A paper about the cipher

A good paper on the cipher, written (and translated? from Chinese) by Whitfield Diffie and George Ledin, offering a comprehensive explanation, is available at the following link: https://eprint.iacr.org/2008/329

This paper also includes some of the design choices and explains how the S-box was created.

My YouTube video about the cipher

Of course, I also made a YouTube video for my “Cryptography for everbody” YouTube channel :-). You can watch it here:

The Chinese Cipher ShāngMì 4 (SM4 ,商密4) Explained

Simplified AES (S-AES) Cipher Explained: Understanding Cryptographic Essentials

In the world of cryptography, security and simplicity are often at odds. But what if there was a way to bridge the gap between understanding cryptography and actually doing robust encryption? A few months ago, I found out that there is a simplified version of AES, called Simplified AES (S-AES). It is a very intriguing cipher intended as a teaching tool, analogous to Simplified DES (S-DES) for DES (which I had already implemented in CrypTool 2 many years ago). I implemented S-AES as a new CrypTool 2 component and also created a YouTube video about the cipher (see end of blog article). Also, my blog article here explains the main components of S-AES, breaks down the two rounds, and demonstrates the basic operations. I also suggest that if you really want to know how the cipher works, in addition to reading the article and watching my YouTube video, you implement the cipher yourself. As for me, I don’t understand a cipher 100% until I implement it myself :-).

We’ll start with an overview of the cipher. The following figure therefore shows the complete algorithm:

Overview of the complete simplified AES algorithm
Simplified AES Algorithm taken &
modified from [1]

S-AES is a block cipher and it has a keysize of 16 bit and a blocksize of 16 bit. It consists of two rounds and a key expansion, which generates two additional round keys based on the provided 16-bit key. The first round consists of four building blocks, while the last round only uses three of these. In the following, we first shortly discuss the history of the S-AES cipher and after that each of the building blocks. Finally, we have a look at the key scheduling.

1. The S-AES Cipher

Simplified AES, or S-AES, made its debut in 2003 thanks to the work of Musa et al. [2]. Just like its more complex counterpart, the Advanced Encryption Standard (AES), S-AES is a block cipher. However, it is designed primarily for educational purposes, making it a learning tool for the classroom. While AES operates on 128-bit blocks and employs 128, 192, or 256-bit keys, S-AES works with 16-bit blocks and 16-bit keys. Furthermore, S-AES comprises only two rounds, as opposed to AES, which has 10, 12, or 14 rounds depending on the key length [1]. This design allows cryptography enthusiasts to grasp the core concepts without the overwhelming complexity of AES.

[1] Holden Joshua, Rose Hulman Institute of Technology ” A Simplified AES Algorithm “. 2010 (Figures by Holden)
[2] Musa, Mohammad A., Edward F. Schaefer, and Stephen Wedig. “A Simplified AES Algorithm and its Linear and Differential Cryptanalyses“. Cryptologia 27.2 (2003): 148 177.

2. AddRoundKey Operation

The first step in an S-AES round is AddRoundKey. This operation involves XORing a 16-bit round key onto the 16-bit state. The state is shown here always as 4×4-table, each cell contains a nibble and the first column is the first byte and the second column is the second byte. XORing is a bitwise operation that combines the bits of two inputs, returning a new value based on their differences. Consider the following example:

AddRoundKey operation

In this case, each corresponding bit of the state and the round key is XORed together, producing the result 4E 52. Example XORing of a single state nibble:

Example XORing of a single state nibble

3. SubstituteNibbles Operation

Next up is SubstituteNibbles, which applies a 4-bit S-box to the 16-bit state. The S-box is a lookup table that replaces each 4-bit input with a corresponding 4-bit output. For instance:

SubstituteNibbles operation

The S-AES 4-bit S-box is a key element of this operation, performing a specific substitution for each possible 4-bit input value. An example S-box lookup for a specific value looks like:

Example S-box lookup for a specific value

The corresponding S-box table is defined as follows:

S-AES s-box table

4. ShiftRows Operation

ShiftRows involves exchanging the last two nibbles of the 16-bit state. It’s important to note that this operation is self-inverse, meaning it can be reversed to decrypt the data. For example:

ShiftRows operation

An example computation of ShiftRows looks like:

Example computation of ShiftRows

This is the only primitive, which is self inverse. All other primitives have an inverse which is used for decryption instead of the encryption primitive.

5. MixColumns Operation

MixColumns applies a matrix operation on the 16-bit state within the Galois field GF(16). This operation can be quite complex, but it’s essential for ensuring strong encryption. For example:

MixColumns operation

It uses the reducible polynomial 𝑥^4+𝑥+1 for GF(16).

The matrix to mix the columns is is:

MixColumns matrix

An example computation of both state bytes looks like:

Example computation of a single byte

The matrix multiplication is performed within GF(16). Best is to use a precomputed lookup table for the multiplication. To see how computing in finite fields works, have a look at https://en.wikipedia.org/wiki/Finite_field.

6. KeyExpansion

Inspired by the AES key expansion algorithm, S-AES’s ExpandKey operation computes round keys for each round. It employs a round constant array (Rcon) to generate the necessary keys. For instance, roundKey1 and roundKey2 can be computed using this scheme:

KeyExpansion scheme

And the g function is defined as follows:

KeyExpansion g function

7. YouTube Video

If you want some more explanations and details, please have a look at my YouTube video about S-AES, where I explain each step in more detail:

The Simplified Advanced Encryption Standard (S-AES) Explained

Cryptography for everybody: I Created a Text-Based AES-Like Cipher – A Cipher Built Using Only Classical Ciphers

Can you build a cipher with the structure of the Advanced Encryption Standard (AES), our current standard modern symmetric cipher, but only use classical ciphers? I asked myself this question when I implemented AES in C# as a preparation for my upcoming AES videos on my YouTube channel in 2021.

AES’ structure (10 rounds for AES-128) consists of 4 different building blocks:
1) AddRoundKey,
2) SubBytes,
3) ShiftRows, and
4) MixColumns:

AES structure

The AddRoundKey building block adds a round key to the state array of 16 bytes (or plain and/or ciphertext) using XOR. The SubBytes building block substitutes each byte using AES’ S-Box, the ShiftRows building block performs a shift of the rows of the state array, and the MixColumns building block mixes the columns of the state array by multiplying each “vector” with an invertible matrix in the finite field GF(2^8).

When I implemented each of these four steps, I was reminded of some classical ciphers: AddRoundKey reminded me of an additive cipher, SubBytes reminded me of a simple substitution cipher, MixColumns reminded me of a transposition cipher, and the matrix multiplication finally reminded me of a Hill cipher.

Thus, I changed the inputs (plaintext and key) and the output (ciphertext) of the AES to simple text (just letters from A to Z), exchanged AddRoundKey with an additive cipher (using MOD 26), exchanged SubBytes by SubBigrams (a bigram substitution cipher), I kept ShiftRows as it was, and exchanged MixColumns with a 4×4 Hillcipher (also using MOD 26). The “TextAES” was born :-).

To also allow decryption, I computed the inverse S-Box (an inverse lookup table for the bigram substitution cipher) and an inverse matrix for the Hill cipher.

I kept the key expansion more or less as it was, but with text, and also used the bigram substitution and replaced its round constants by “AAAA”,”BAAA”,”CAAA”, etc.

Finally, I was convinced that you can create an AES-like cipher using only classical ciphers :-).

If you are interested in details of this self-made crazy cipher, have a look at the video I made about it:

I Created a Text-Based AES-Like Cipher

If you are interested in details of the real AES, you may also have a look at my other two videos about AES and AES key schedule:

AES – The Advanced Encryption Standard Explained
AES – Key Schedule/Key Expansion Explained

Also, if you want to play with my source code in C# of AES and TextAES, you can find it freely available on GitHub: https://github.com/n1k0m0/AES-and-Text-Based-AES

Finally, here is the original publication of AES:
Daemen, Joan, and Vincent Rijmen. The design of Rijndael. Vol. 2. New York: Springer-verlag, 2002.

Nils