The annals of World War II are replete with tales of ingenious inventions, some designed to bring destruction, and others to guard secrets. Among the latter is the SZ42, or “Schlüsselzusatz 42,” a German rotor encryption machine. I was always fascinated of this machine, which is one of the first “stream ciphers” you could say. Since we had no implementation in CrypTool 2, I created an implementation based on the very good descriptions of the cipher written by my friend George Lasry. Also, I made a YouTube video about the machine which you can find at the end of this article.
Of course, I also wanted to write a blog article (this one here :-)), which shows all the components of the machine in detail. Therefore, in this article we’ll unravel the mysteries of the SZ42, exploring its history, inner workings, and the encryption it offered during wartime.

Image from Wikipedia taken in Bletchley Park Museum
Introduction to the SZ42
The SZ42, short for “Schlüsselzusatz 42,” translates to “cipher attachment 42” in English. It was one of Germany’s cryptographic machines deployed during World War II. Notably, there were several models of this machine, including the SZ40 and SZ42, along with variants like SZ42a, SZ42b, and SZ42c. The Germans called it “Sägefisch” (“sawfish” in English), while at Bletchley Park, it went by the codename “Tunny,” akin to a tunafish.
Developed by the German company “C. Lorenz AG,” the SZ42 served the role of encrypting radio teletype (RTTY) communications. It began with an experimental link using SZ40 machines in June 1941, but it was the enhanced SZ42 machines that came into substantial use from mid-1942 onwards, primarily for high-level communications.
2. Baudot Code
To understand the SZ42’s significance, we must first delve into the Baudot code, the lingua franca of early teleprinter communications. Émile Baudot invented this pioneering bit-based code in the 1870s. It preceded the International Telegraph Alphabet No. 2 (CCITT-2), the most common teleprinter code before the advent of ASCII.
Baudot code words are composed of 5 bits, allowing for a total of 32 possible code words. However, this proved insufficient for encoding letters, digits, and special characters. To circumvent this limitation, Baudot introduced special symbols known as “figure shift” and “letter shift” to alter the code word representation. The version of Baudot code used in the SZ42 was the “Baudot-Murray-Code,” which optimized code assignments for commonly used letters, reducing strain on the teletypewriter mechanics.
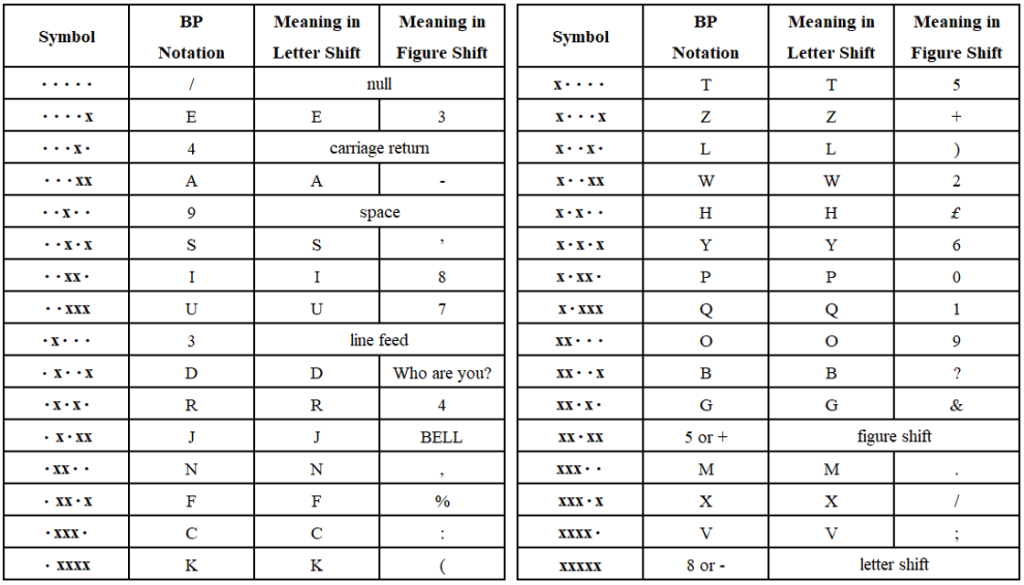
3. How Does the SZ42 Encryption/Decryption Work?
The SZ42 operated by encrypting and decrypting Baudot code transmitted and received by teletype printers. It accomplished this by generating a “pseudo-random” stream called K, consisting of 5-bit code words, which was then XOR-ed with the plaintext (P) or ciphertext (C).
Encryption: C = P ⨁ K
Decryption: P = C ⨁ KThis method marks the SZ42 as one of the early stream ciphers, a critical precursor to modern encryption techniques.
4. The Inner Mechanism of the SZ42
The SZ42 boasted an intricate design with a total of 12 wheels, categorized into Chi, Psi, and Mu wheels. Each wheel had a unique pin count, with the Chi wheels having 41, 31, 29, 26, and 23 pins, Psi wheels with 43, 47, 51, 53, and 59 pins, and the Mu wheels with 61 and 37 pins.
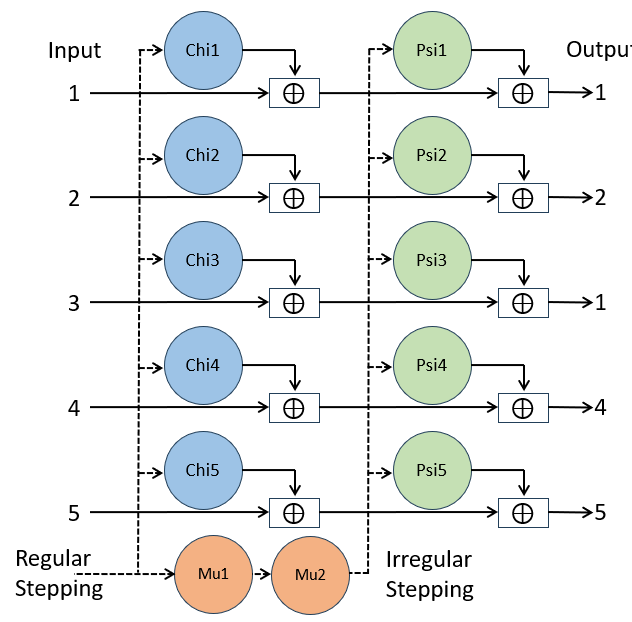
Whenever a pin was in an active position, it added a 1 to the keystream, while in inactive position it added a 0. For each of the 5 Baudot bits, there were one Chi, and one Psi wheel.
The Chi wheels stepped regularly after each encryption, whereas Psi wheels stepped irregularly if Mu2 had an active pin, with Mu1 also stepping regularly after each encryption. Mu2 only stepped when Mu1 had an active pin.
5. Key Generation and Motor Limitations
Key generation in the SZ42 was governed by specific rules for setting the allowed numbers of active pins on each wheel. For example, Chi wheel 1 had a rule like “Allowed number of crosses in Chi1 is 20 or 21.” These rules ensured the machine operated effectively.
Motor limitations, like “CHI2_1BACK,” were introduced to make cryptanalysis more challenging. They compelled Psi wheels to move at specific positions, increasing the complexity of decryption. These limitations aimed to reduce the number of motor stops for Psi wheels, enhancing the machine’s security.
For details have a look at: James Reeds, Whitfield Diffie, and J.V. Field. 2015. Breaking Teleprinter Ciphers at Bletchley Park: An Edition of I.J. Good, D. Michie and G. Timms: General Report on Tunny with Emphasis on Statistical methods (1945). John Wiley & Sons.
6. Keyspace Size and Unicity Distance
The SZ42’s keyspace size without any wheel setting rules was staggering:

Considering these immense sub-keyspaces for each wheel-set, the total keyspace size reached:

This immense keyspace made brute-force attacks infeasible.
Furthermore, the SZ42 had a unicity distance U of 157, making it an incredibly secure encryption tool. Unicity distance can be camputed by dividing the Entropy of the keyspace by the redundancy of the (English) language:
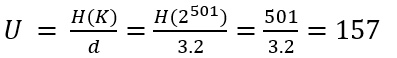
Unicity distance is a concept in cryptography that refers to the minimum amount of ciphertext (encrypted text) required for an attacker to uniquely determine the corresponding plaintext (original message) while performing a brute-force attack. Since there are no “half” letters, the unicity distance value is always rounded up. With the (non-key rules-restricted) SZ42 a minimum number of 157 letters is required to obtain only one single valid solution when performing an attack. With less letters, we obtain multiple plaintexts and we can not distinguish which one is the correct one.
7. Conclusion
The SZ42 cipher machine stands as a testament to the ingenuity of its time, showcasing advanced encryption techniques during World War II. Its large keyspace and wheel-based encryption made it a challenging adversary for codebreakers. This machine’s historical significance and cryptographic complexity serve as a testament to the ever-evolving world of encryption and information security. Nevertheless, using Colossus, one of the first “computers”, the code breakers of Bletchley Park were able to frequently break into the encryption offered by the SZ42. Today, using modern techniques like hillclimbing and simulated annealing, we are also able to break the cipher
8. A YouTube Video About the SZ42
I also made a YouTube video about the SZ42 which you can watch here:
