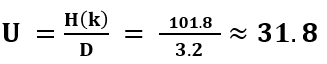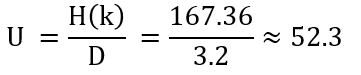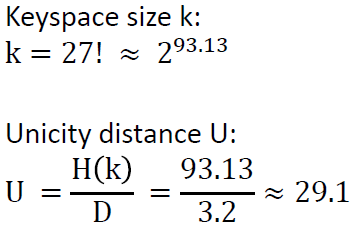The Typex is a cipher machine used by the British during World War II. It is, similar to the German Enigma cipher machine, an elector-mechanical rotor encryption machine. In contrast to the Enigma, the Typex was not broken during WWII. The Germans believed that Enigma is unbreakable and since Typex is very similar, they did not even attempt to break the machine.
I recently wrote a new CrypTool 2 component that implements the Typex cipher machine. If you are interested in testing the component (and the machine) yourself, you should download the latest nightly build of CrypTool 2.
History and Usage of the Typex
The Typex machine was used for
a) Encryption of the own communication
b) Deciphering German Enigma messages
It was developed by Wing Commander Oswyn G.W. Lywood, Flight Lieutenant Coulson, Mr. E. W. Smith, and Sergeant Albert Lemon.
This image here shows Oswyn George William Gifford Lywood; a photo by Walter Stoneman; bromide print, February 1945; NPG x186070 © National Portrait Gallery, London.
There were several different versions of Typex including: Typex Mark I up to Mark VIII, Mark 22 and Mark 23.

A very nice and more detailed overview of the history of Typex can be found here: https://typex.virtualcolossus.co.uk/typex.html
The Typex Components
In the following, we have a look at the machine’s components. The Typex machine consists of:


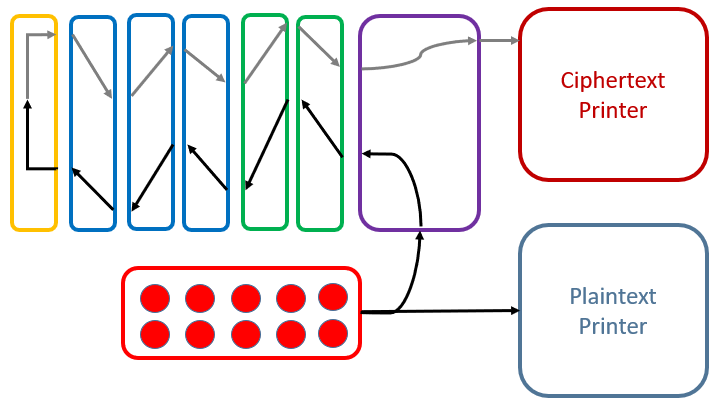
When pressing a key on the keyboard, the plaintext letter is printed by the plaintext printer. Also, current flows through the plugboard, the two stators, the three rotors and is then reflected by the reflector. Then it flows back through the three rotors and the two stators as well as the plugboard. Finally, the ciphertext letter is printed by the ciphertext printer.
Clearly, every time a key is pressed, between one and all three rotors move (Stators of course don’t move). In contrast to Enigma, a Typex rotor moves much more often. This is because the rotors have between 4 and 7 notches, while Enigma rotors had at most two notches.
The Typex Plugboard
The Typex plugboard is the first (and last) component (despite the printers), which current is lead through after a key is pressed on the keyboard. It allows to “plug” letters, creating an initial monoalphabetic substitution.
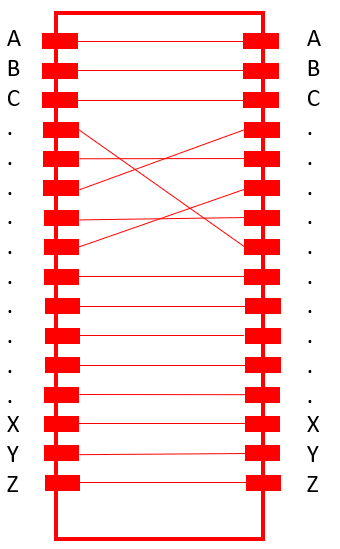
The plugboard is not reciprocal (like the Enigma‘s plugboard. With Enigma, if we have letter X to letter Y, then we would also have letter Y to letter X). It, thus, offers a larger keyspace than Enigma’s plugboard.
The Typex Rotors/Stators
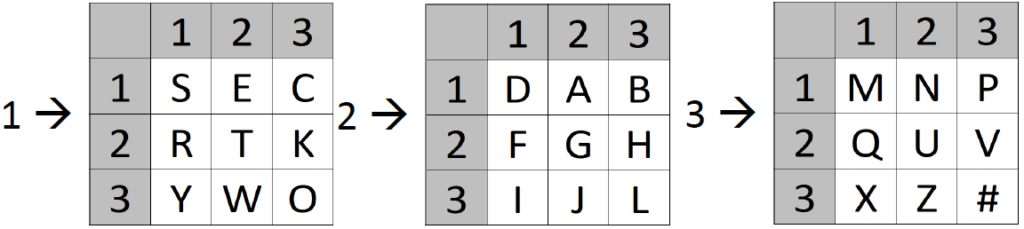
Typex consists of two stators and three rotors. A rotor has more „notches“ than Enigma rotors (in CrypTool 2’s Typex implementation between 4 and 7). A rotor’s electrical contacts are doubled to improve reliability. Unfortunately, the original rotors are not published and still kept secret, thus, the simulators use no official rotor definitions.
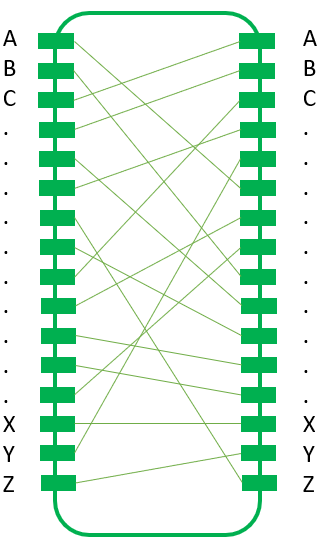
The Typex Reflector
The Typex reflector “reflects” the current coming from the rotors back through the rotors. In later Typex versions the reflector was replaced by an additional plugboard which allowed to change the reflector’s wiring easily.
Keyspace Size and Unicity Distance
Since no original rotor definitions are known, the computation of keyspace size and unicity distance is based on the “CyberChef” Typex simulator written and published by GCHQ (see https://gchq.github.io/CyberChef/).
With this implementation, we have to choose 5 rotors (3 actual rotors and 2 stators) from a set of 8 rotors. Since a rotor can be put into the machine in forward or reversed position, they basically doubled the amount of usable rotors to 16. Here, we assume that we can use each rotor as many times as we like in parallel. Thus, the “rotor keyspace size” is:
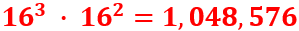
We have to set the rotor start positions. We have five rotors (3 actual rotors and 2 stators). Each rotor can be in one of 26 different positions (A-Z). Thus, we have a total “start position keyspace” of:
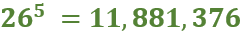
The plugboard is basically a simple monoalphabetic substitution cipher. That means, for the first letter we have 26 different letters to choose from, for the second letter, we have 25 different remaining letters to choose from,…
Thus, the “plugboard keyspace” is:

To compute the overall keyspace size, we have to multiply all “sub-keyspace” sizes:

To compute the unicity distance U, we have to divide the entropy of the keyspace by the redundancy of the (English) language:
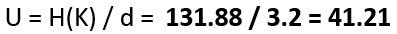
This means, we need a minimum of 42 letters to be able to obtain a single valid solution when we perform cryptanalysis of a Typex message.
A YouTube Video about Typex and a Web-Based Simulator
I also created a YouTube video about the Typex cipher machine. Here, I discuss the machine as well as its keyspace size and unicity distance. Also, I show how to use the Typex component in CrypTool 2:
Finally, if you want to “play” with a really nice simulator (and also want to learn much more about the Typex), you should have a look at the “Virtual Typex”: https://typex.virtualcolossus.co.uk/Typex/
The usage of the simulator is also shown in the above linked YouTube video :-).