I recently made two videos about two interesting classical ciphers invented by Félix Marie Delastelle. Delastelle wrote a book on cryptography in 1901. Unfortunately, he died before his book was published in 1902. In his book, he describes several ciphers he invented. This blog post is about two of them: the bifid cipher and the trifid cipher.
The Bifid Cipher
The bifid cipher is a cipher which combines a Polybius square with transposition, and uses fractionation:
1. First, we use a keyword to create a 25-letter Polybius square
For example: “SECRET KEYWORD”:
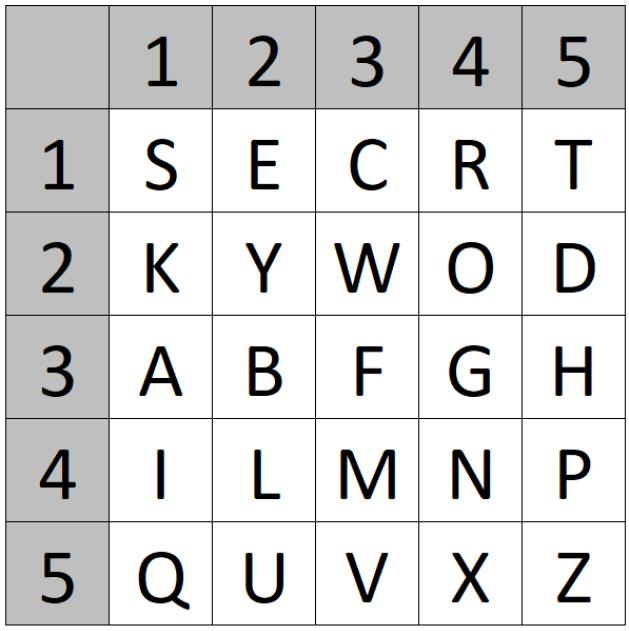
2. Then, we encrypt the plaintext using the square, by writing the coordinates of the square below the plaintext. Example:
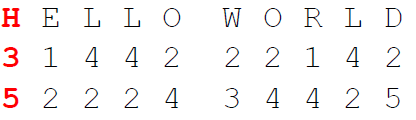
3. After that, we write the digits (transposed/fractionated) in a single row:

4. Finally, we decrypt the digits using the square to obtain the ciphertext:
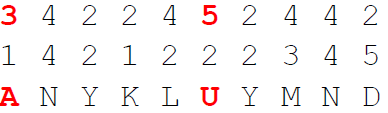
The decryption is the reverse process. It is also possible to not encrypt the plaintext in one go. Instead, you can encrypt the ciphertext in blocks of n (n for example being 5).
The keyspace size and unicity distance (minimal number of letters needed in a ciphertext that allows having only a single valide solution) can be computed as follows:

The Trifid Cipher
The trifid cipher was invented by Félix Marie Delastelle as an extension of the above shown bifid cipher.
1. First, we use a keyword to create three 9-letter Polybius squares. For example: “SECRET KEYWORD”
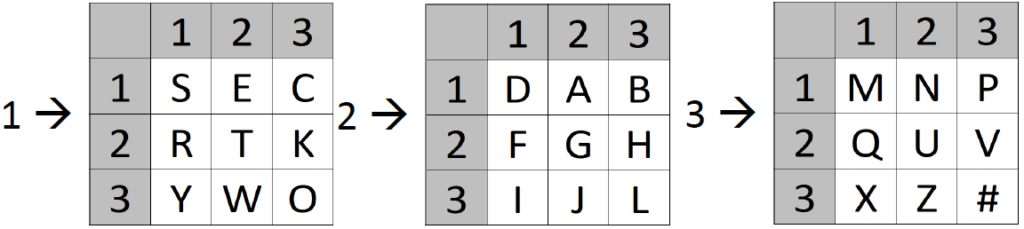
2. Then, we encrypt the plaintext using the squares, by writing the number of the used square number and the coordinates below the plaintext. Example:
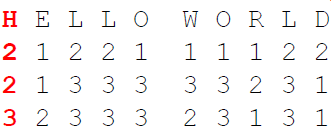
3. After that, we write the digits (transposed/fractionated) in a single row
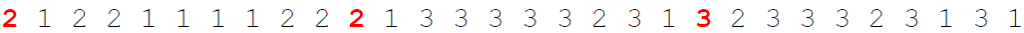
4. Finally, we decrypt the digits using the three squares:
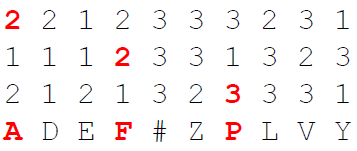
The decryption is the reverse process. It is also possible to not encrypt the plaintext in one go. Instead, you can encrypt the ciphertext in blocks of n (n for example being 5).
The keyspace size and unicity distance (minimal number of letters needed in a ciphertext that allows having only a single valide solution) can be computed as follows:
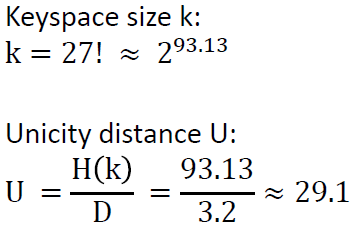
YouTube Videos about the Bifid and Trifid Ciphers
I made a YouTube video about the Bifid cipher. Here, you can also see how to use the bifid cipher component of CrypTool 2:
I also made a YouTube video about the Trifid cipher. Here, you can also see how to use the trifid cipher component of CrypTool 2:

Hello ! I wonder the Trifid cipher by dCODE.fr’s Trifid cipher.
I make with pen the cipher and my result is FALRALBXUOXMLF. It is same as with Cryptool2. dCODE.fr result is FRKCQAFLWINZSZ. I use the last letter #. Same to dCODE.fr. There is standard _ but I change it.
What make I wrong?
Best regards
Jussi
ps. I dont find Your email adress
Hello Jussi,
I think you should write to the author of the fantastic dcode.fr webpage and ask him directly the same question. I think he should know what is different. Maybe they have a bug or you do something wrong when using their page. You can find contact information of him here: https://www.dcode.fr/a-propos
PS: Usually, as with all the ciphers in CrypTool 2 which I implemented especially for my videos, I test them using the great implementations on http://www.kryptografie.de, which is maintained by Oliver Kuhlemann (see https://kryptografie-de.translate.goog/kryptografie/chiffre/trifid.htm?_x_tr_sl=de&_x_tr_tl=en&_x_tr_hl=de). But even there the ciphers sometimes have small bugs, which I then report to Oliver 🙂
Kind regards,
Nils
Thank You for information.
Br
Jussi