Tag: CrypTool 2

I Implemented the “Mexican Army Cipher Disk” and also its Cryptanalysis in CrypTool 2

In the last view days, I implemented the Mexican Army Cipher Disk and its cryptanalysis in CrypTool 2. I also made a YouTube video about that (see below in this blog post).

The Constitutionalists in Mexico used the Mexican Army Cipher Disk at the beginning of the 20th century during the Mexican revolution. It is a homophonic substitution cipher, but rather weak. For encrypting a letter, you have either a 3-symbol or a 4-symbol homophone group, with a total of 100 homophones (01 to 00).

My self-created Mexican Army Cipher Disk

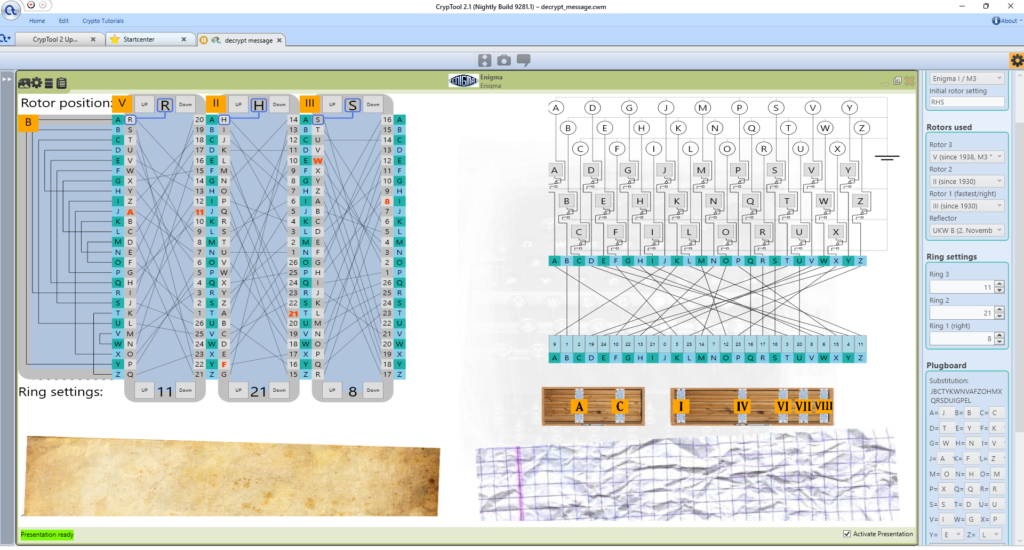
The groups are created using the disk device, which consists of 5 disks (see shown figure above):
• The outer disk contains the Latin alphabet
• Four inner disks contain 2 digits numbers
• Four inner disks can be turned

The key of the cipher is the rotation of the four inner disks and can be described in two ways:
1) The digit groups below the letter A : 01, 27, 53, 79
2) With four Latin letters ; each letter is the one above the first digit group of the corresponding disk: A, A, A, A

Build your own Mexican Army Cipher Disk

Now, if you want to also build your own cipher disk, you may use my self-created template here:

Mexican-Army-Cipher-DiskDownload

Since I used powerpoint to create the template, the angles are not 100% perfect, but it still works well. You need to print it five times and always cut a smaller disk out of each printout. To get more stability, you may also use some cardboard and glue the disks onto these before assembling the device. Finally, all the disks are placed on top of each other. I used a paper clip that I bent and put through all the slices.

Cryptanalysis

If we want to break the Mexican Army Cipher Disk, it is a rather easy task. By hand, we just search in each number group (01 to 26, 27 to 52, 53 to 78, and 79 to 00) for the most frequent homophone. This stands probably for the letter E. Move your disks to all found E positions and you should be able to decrypt your ciphertext.

If you don’t want to break it by hand, you can use CrypTool 2 and the “Mexican Army Cipher Disk Analyzer” component for automatic cryptanalysis. It performs a brute-force attack and searches through all disk settings. Here, with the help of a language model (e.g. English pentagrams) it scores each of the decrypted texts. The correct plaintext should be on the first position of the best list of the analyzer.

YouTube Video

I alse created a YouTube video about the Mexican Army Cipher Disk. You may watch it here:

My YouTube video about the Mexican Army Cipher Disk

Some References

I Deciphered a Radio-Transmitted Enigma Message

On Saturday the 23rd July 2022, the Maritime Radio Historical Society (MRHS) and the Cipher History Museum sent an Enigma-encrypted radio transmission via the KPH stations. I was able to receive the message and decrypt it using CrypTool 2. Message was sent via Morse (CW) frequencies and radioteletype (RTTY) frequencies.

In one of my YouTube videos, I explain how I received the message using KiwiSDR and how the Morse decoding in KiwiSDR and the decryption process in CrypTool 2 worked. I thank Tom Perera from the cryptocollectors group for providing the playbacked parts of the original audio recording of the transmission. Finally, I recorded the wrong audio device, thus, I only had the video recording of what I did.

I Decrypted an Enigma Message Transmitted by Radio

Despite not being the fastest decipherer, I am proud that I received a very nice certificate. I got it after sending the plaintext to the Martitime Radio Historical Society via email:

My certificate for deciphering the Enigma message from the MRHS

If you want to try to decrypt the Enigma message on your own, here is my received and Morse-decoded message (actual ciphertext in bold):
FQ CQ DE KPH KPH KPH CQCQ CQ DE KPH KPH KPH CRYPTO MESSAGE FOLLOWS bt HQTRS FR FOCH 1914Z bt 100 bt BRV LTV bt VCXTY JRVHA NNKMO FGKIG OIPLM KVHVZ WDMIP XWRBX JKDWT KGZZA IWJVN QUTJF HPPWG KEDDQ QFEMT UKMQU IDIGF YUAJB RPPWS IBJCV EI[err][err]E CQ CQ CQ DE KPH KPH KPH CQ CQ CQ DE KPH KPH KPH CRYPTO MESSAGE FOLLOWS bt HQTRS FR FOCH 1914Z bt 100 bt BRV LTV bt VCXTY JRVHA NNKMO FGKIG OIPLM KVHVZ WDMIP XWRBX JKDWT KGZZA IWJVN QUTJF HPPWG KEDDQ QFEMT UKMQU IDIGF YUAJB RPPWS IBJCV E 5IH[err][err][err][err]EN SVAM bt I[err]

You can decrypt it using CrypTool 2 or any Enigma simulator. Here is a screenshot of the Enigma and settings in CrypTool 2:

Enigma set up for decryption of the message in CT2

Some references:

– To visit the MRHS, please go to: https://www.radiomarine.org
– The Cipher History Museum go to: https://cipherhistory.com/
– KiwiSDR you can find here: http://kiwisdr.com

Cryptography for everybody: Zero-Knowledge Proofs and Protocols Explained

In my newest video on “Cryptography for everybody”, I explain how zero-knowledge proofs and protocols work. A zero-knowledge proof or protocol is a method by which one party (usually Peggy P) can prove to another party (usually the verifier Victor V) that they know a value (e.g. a secret key or password) without actually revealing it.

First, we discuss the classical cave example by Quisquater: Here, Peggy wants to prove to Victor that she knows how to open a secret door in a cave. But only to Victor and not to anyone else.

Then, we have a look at a real zero-knowledge protocol: the Fiat-Shamir Protocol. This protocol works with modular arithmetic. Peggy has to create a private key s and register her public key v = s² with a trusted third party. Then, Victor can challenge her with a simple protocol. How this works, I explain in the video.

Finally, we have a look at the zero-knowledge simulation in CrypTool 2. Watch the video here:

Zero-Knowledge Proof Explained

“Cave” paper by Quisquater: Quisquater, Jean-Jacques, et al. “How to explain zero-knowledge protocols to your children.” Conference on the Theory and Application of Cryptology. Springer, New York, NY, 1989.

Feige-Fiat-Shamir protocol: Feige, Uriel, Amos Fiat, and Adi Shamir. “Zero-knowledge proofs of identity.” Journal of cryptology 1.2 (1988): 77-94.

Cryptography for everybody: Some work on the Random Number Generator Component and XORShift

Comparation of the new XORShift component in CrypTool 2 with 8 bit, 16 bit, 32 bit, and 64 bit

I spend some time on the Random Number Generator component of CrypTool 2. The component allows the generation of random numbers. The output format can be set to byte array, (big) integer, integer array, or just a random bool 🙂

One of my students implemented the component a few years ago. I realized, that the component did not output the random numbers directly. Instead, it created “new” random numbers by a creating single bits per random number. The bits then were used to create the output data. Since people should get what they selected I changed the code. Now, it directly outputs the original random numbers. Also, the generation was not very fast. It “wasted” a lot of bits. You needed to create 8 random numbers for a single 8 bit random number.

Old and new random number generators

Speaking of generators: the component offers different pseudo random number generators. For example linear congruential generator, inverse congruential generator, and x^2 mod N. It offers also the standard .net Random.random as well as the cryptographic random number generator RNGCryptoServiceProvider. For the generation of cryptographic keys and IVs this should always be used.

Additionally, I added the “XORShift” random number generator with 8 bit, 16 bit, 32 bit, and 64 bit. The XORShift takes the previous number and XORes it three times with a shifted value of itself. For example, the 8 bit XORShift can be implemented with five shifts to the left, three shifts to the right, and seven shifts to the left:

_state = (byte)(_state ^ (_state << 5));
_state = (byte)(_state ^ (_state >> 3));
_state = (byte)(_state ^ (_state << 7));

In a similiar fashion, I implemented 16 bit, 32 bit, and 64 bit. Wikipedia contains many other versions of XORShift. These I will probably implement in the near future. For fun, I created a comparision using images of all XORShift implementations we have in CT2. The figure at the beginning of thist blog post shows this comparision. As you can see, XORShift 16 already looks “very” random. That is because of its period of 2^16, meaning, after 2^16 iterations the numbers repeat.

Test it and read more about XORShift

You can test the new XORShift in the new nightly build of CT2. Also, if you are interested in more details about XORShift, I recommend reading the nice Wikipedia article here: https://en.wikipedia.org/wiki/Xorshift. XORShift is also really nice for creating random numbers on old 8 bit machines like the C64. Its easy to implement, fast, and “random enough” for games :-).

Nils

Cryptography for everybody: Safe primes for RSA?

Generation of “safe” primes in CT2 using the RSA KeyGenerator component

I recently got some interesting feedback to the “Break reduced RSA” YouTube video I made some time ago. Of course I used CrypTool 2 (CT2) in that video. One viewer asked me, why we chose to generate non-safe primes, as well as if the quadratic sieve component of CT2 is able to break RSA challenge numbers. My answer to the second question: Since we have a quite old implementation of msieve (the library we use) converted to C# long ago, I don’t think the factorization algorithm is as powerful as the current state-of-the-art factorization libraries. Nevertheless, it is “good enough” to show how to break RSA (up to N in range of 2^300).

The answer to the safe prime question: Good question! I never thought of generating such numbers in CT2 and thought standard prime numbers are ok for CT2. I mean, it is a tool for education and not meant for any security purposes. Nevertheless, in real world applications you use large primes for RSA with additional requirements: They should be safe. So I updated the RSA KeyGenerator component to also allow the generation of safe primes. But are safe prime numbers still needed with RSA modules in the range of 2^2048 and above? For the current state-of-the-art of RSA factorization, you may have a look at https://en.wikipedia.org/wiki/RSA_Factoring_Challenge.

But what is a safe prime?

A number p is a prime number, if it is only divisible by itself and by 1. For example 13 is a prime number, or 17, or 23, … etc. A “safe prime” number p is a number, that is prime AND (p – 1) / 2 is also a prime number which we then call a Sophie Germain prime. An example for a safe prime is 23, because (23 – 1) / 2 = 11 is a Sophie Germain prime. Safe prime numbers are more resistant against some factorization methods, which could be used to factorize the RSA’s N (which is the product of two large primes p and q).

But are safe primes really needed for RSA?

I questioned that myself and found a paper by Rivest, who is the R in RSA. Already in 1999, Rivest stated that: “We find that for practical purposes using large “random” primes offers security equivalent to that obtained by using “strong” primes. Current requirements for “strong” primes do not make them any more secure than randomly chosen primes of the same size. Indeed, these requirements can lead a general audience to believe that if a prime is “strong” that it is secure and that if it isn’t “strong” then it must be “weak” and hence insecure. This simply is not true.” [1]

Rivest speaks about “strong” primes, not about safe primes. Strong primes have additional properties, from which “safe” primes fullfil one. But today, the usage of just “random” primes is good enough to keep RSA secure, since the primes are so large, that the properties for “strong” and “safe” are negligible. The “safe” property for primes was introduced to counter special factorization algorithms, like Pollard-Rho. But the modules we use today with RSA are too large to be factored with e.g. Pollard-Rho.

Nevertheless, now we have the choice in CT2 to generate either “random” or “safe” primes. Also, the RSA KeyGenerator uses a cryptographic random number generator during the generation of the RSA keys. In the CT2 workspace shown at the beginning of the blog article, we generate a 1024 bit RSA key and set the generator to “safe” prime generation. The prime test components evaluate the generated primes p and q and if both are “green” this means that the primes are safe.

You may be interested in my RSA YouTube video:

Basics of Cryptology – Part 11 (Modern Cryptography – Asymmetric Ciphers – RSA)


And you may also be interested in my “How to break reduced RSA” YouTube video:

Break (Reduced) RSA Using Factorization


[1] Rivest, Ronald L., and Robert D. Silverman. “Are Strong Primes Needed for RSA?” IN THE 1997 RSA LABORATORIES SEMINAR SERIES, SEMINARS PROCEEDINGS. 1999.

Nils

Cryptography for everybody: I updated the Transposition Analyzer in CrypTool 2 to Make it More Convenient

Today, I updated the “transposition analyzer” component of CrypTool 2 (CT2) to make its usage more convenient. The analyzer allows the cryptanalysis of ciphertexts that are encrypted using the columnar transposition cipher. It was written some time ago in the early days of CT2 by some of my commolitons when I was doing my masters.

The CrypTool 2 transposition analyzer component now supports keylength ranges


It always bugged me that you needed to restart the analyzer when you wanted to analyze different key lengths. For example, if you assumed that a ciphertext had been encrypted using a columnar transposition cipher, but you were unsure which key length had been used (e.g. between 5 and 15), you had to restart it for any of the assumed key lengths.

Now, its a matter of setting minimum and maximum key lengths, and the analyzer will test all lengths of the defined range 🙂

Btw, the transposition analyzer supports different cryptanalysis methods/heuristics: brute-force for smaller key lengths, genetic algorithm and hillclimbing for longer key lengths. Also, if you have a crib (a part of known plaintext), the crib analysis can be used.

But besides simply just updating the component, I fixed a few bugs and generally improved the C# code a bit 🙂

If you want to see how to use the transposition analyzer of CT2, I created a video about it in the past:

Break a Columnar Transposition Cipher

Probably, I will also create a new video about columnar transposition ciphers and the updated transposition analyzer in the near future.

We published some years ago a paper about cryptanalysis of the columnar transposition cipher in Cryptologia [1].

Finally, if you want to simply encrypt or decrypt using the columnar transposition cipher, you may have a look at the nice implementation in CrypToolOnline: https://www.cryptool.org/en/cto/transposition

[1] Lasry, George, Nils Kopal, and Arno Wacker. “Cryptanalysis of columnar transposition cipher with long keys.” Cryptologia 40.4 (2016): 374-398.

Nils

Cryptography for everybody: Perceptual Hashing to Compare Images

Some years ago, I supervised a bachelor project with the topic “image processing” at the University of Kassel (when I was working for the “Applied Information Security” group). The bachelor students had to implement image processing components in CrypTool 2.

One result of the project was the so called “ImageHash” component. One of my students implemented the “block hash” by Steinebach [1]. It is a robust (or perceptual) hash function, that allows to use it for the search for images in image databases, even when the image is different (e.g. resized or modified) from the original.

This hash algorithm works in four steps:
Step 1: Grayscale: Colors (RGB) are converted to grayscale (0x00 to 0xFF)
Step 2: Resize: Image is resized to target size e.g. 16×16 pixels
Step 3: Flip: Image is flipped horizontally and vertically until the brightest quarter of the image is in the top left corner
Step 4: Binarize: Convert grayscale pixels to black and white pixels using a threshold

In the following image, an example image is hashed using these four steps:

The four steps of the block hash algorithm

I still like the component and think it was a good addition to CrypTool 2. Clearly, the bachelor students got good grades for the project. Other results were the “Image processor”, the “Transcripor”, and the “Watermark Creator” in CrypTool 2 :-).

Today, I also createad a YouTube video about perceptual hashing. Here, I also show the “ImageHash” component of CrypTool 2 . You may watch it here:

Perceptual Hashing To Compare Images

Nils

[1] Steinebach, Martin. “Robust hashing for efficient forensic analysis of image sets .” International Conference on Digital Forensics and Cyber Crime. Springer, Berlin, Heidelberg, 2011

Cryptography for everybody: Let’s Create Our Own Homophonic Substitution Cipher

In our newest video on “Cryptography for everybody”, we create a homophonic substitution cipher using CrypTool 2.


The “Substitution component” of CrypTool 2 allows to create substitution ciphers. For that, we implemented an easy-to-use syntax based on plaintext and ciphertext alphabets. An “alphabet” is just a string (some text), which consists of our “symbols”. A symbol can be one or more UTF-8 characters.

Example (simple shift cipher):
– Plaintext alphabet=”ABCDEFG…Z”
– Ciphertext alphabet=”BCDEFGH…A”

Providing these two alphabets to the substitution component would create a simple shift cipher, where each letter of the plaintext alphabet is shifted one to the left in our corresponding ciphertext alphabet. In the substitution component, letters are substituted based on their corresponding positions in the given alphabets. The first letter of the plaintext alphabet is substituted by the first letter of the ciphertext alphabet, the second by the second, etc.

But the substitution component is much more powerful. It allows also to create alphabets consisting of “words” and also allows alternative substitutions to create “homophones”.

Example (homophonic substitution cipher):
– Plaintext alphabet=”ABCDEFG…Z”
– Ciphertext alphabet=”[01|02][03|04]…[999|555]”

In this example, the letter A can be substituted by either 01 or 02. The brackets tell the substitution component that it should use everything inside the brackets as a single ciphertext symbol. The pipe symbol tells the component that we want to create alternatives. Using this syntax, we are able to create a homophonic substitution cipher, where one plaintext letter will be replaced by one of the defined homophones.

But we are not only limited to use simple two or three digit combinations. We can also create mappings like [MAXIMILIAN] in the plaintext alphabet and [1001] in the ciphertext alphabet. Doing so, we can create so-called nomenclators. How this can be done in CrypTool 2 is part of the linked YouTube video. So if you are interested in more details, you should have a look at this 🙂

If you are interested in downloading the newest version of CrypTool 2 (I always recommend the nightly build, since it contains the newest components) go to https://www.cryptool.org/en/ct2/downloads

Nils