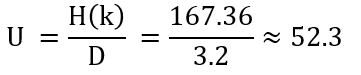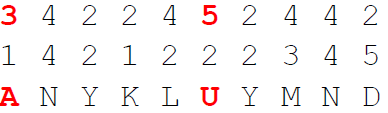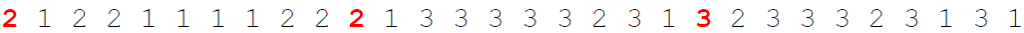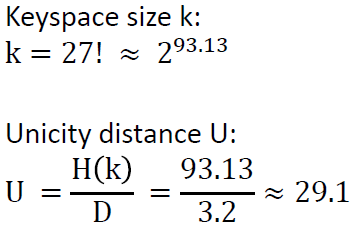The Bazeries cipher was invented by and named after Étienne Bazeries, a French cryptographer. Bazeries was active between 1890 and the First World War.

(21st August 1846 – 7th November 1931)
Bazeries is probably most famously known for the “Bazeries Cylinder”, a cipher device similiar to the Jefferson Disk or the M-94 cipher. Bazeries was a good code breaker: He solved messages encrypted with the official French military transposition system (lead to improvements of the ciphers). He further exposed weaknesses in French cipher systems. He assisted in solving German military ciphers during World War I, after he retired from the army. And in the 1890s he broke the famous nomenclator system called the “Great Cipher”, created by the Rossignols in the 17th century.
How Does the Cipher Work?
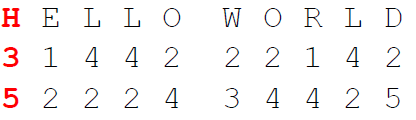
The cipher is a combination of substitution and transposition. For encryption, Bazeries only used a single number key, e.g. 123. In the following, we encrypt an example plaintext (“HELLOWORLD”).
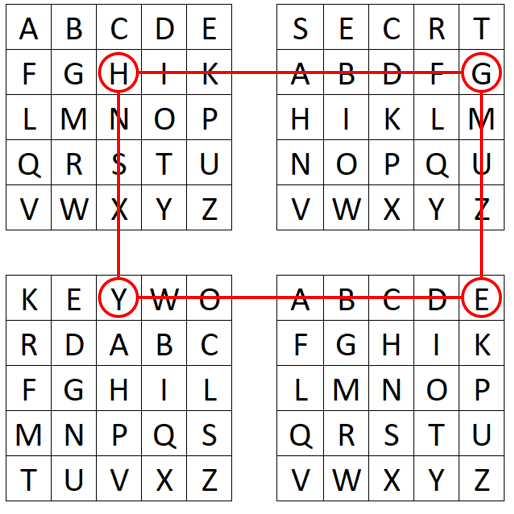
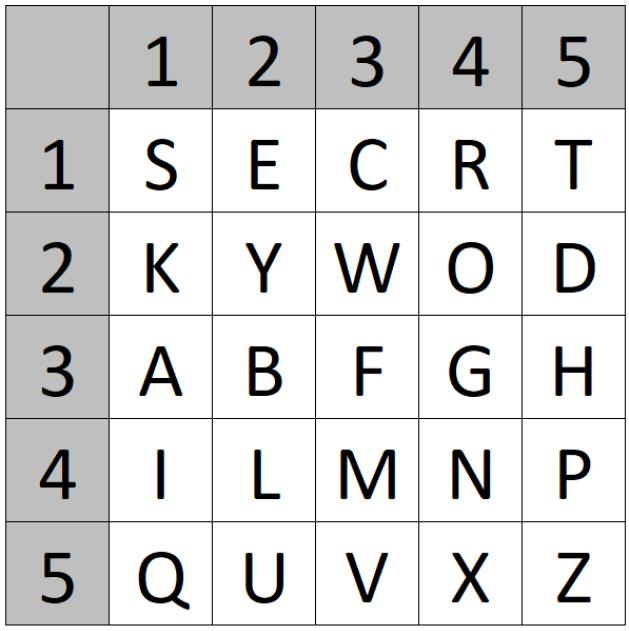
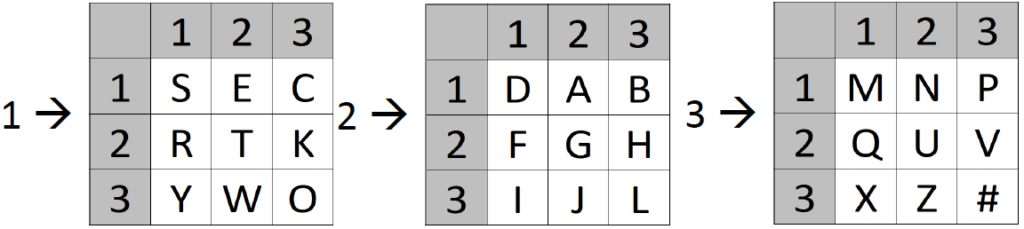
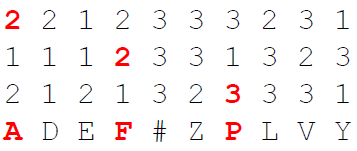
We create two Polybius squares. In the first square, we put the Latin alphabet (I=J; filled from left to right and top to bottom row-wise). In the other square, we write a text representation of the number key, e.g. ONEHUNDREDTWENTYTHREE, followed by the remaining unused letters of the Latin alphabet. We fill the second square from top to bottom and left to right column-wise:
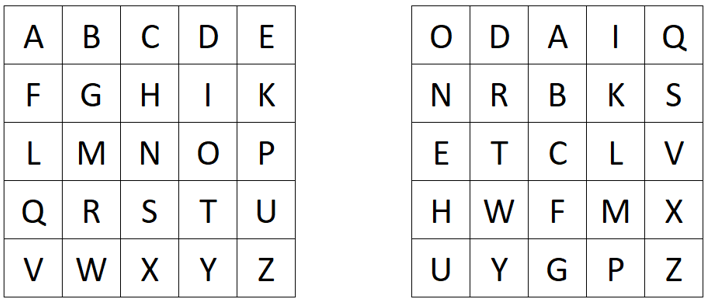
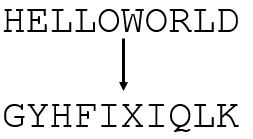
To encrypt a plaintext, we first substitute it using the two created Polybius squares. We look for the plaintext letter in the left square and use the corresponding letter of the right square for the ciphertext (For eample A->O, B->D, etc.). When we encrypt HELLOWORLD, we obtain BQEELYLWEI.
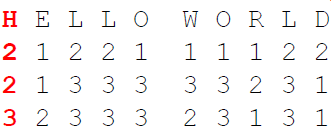
Then, we transpose the intermediate ciphertext using the digits of the number key. We split the text into blocks of sizes defined by the digits of the number key. Then, we reverse each of these blocks to create the final ciphertext:

So our final ciphertext here is BEQYLELWEI. Of course, the decryption is the inverse process of the above shown steps :-).
Keyspace Size and Unicity Distance
Here, we compute the keyspace size as well as the unicity distance (https://en.wikipedia.org/wiki/Unicity_distance). In the original version, as written above, Bazeries created the second Polybius square using the same key as he used for transposition. So for e.g. a maximum number key length of four digits, we compute:
- For a 4-digit key, we have 10^4=10,000 different keys
- For a 3-digit key, we have 10^3=1,000 different keys
- For a 2-digit key, we have 10^2=100 different keys
- For a 1-digit key, we have 10^1=10 different keys
Then, we have to add all these number. Thus, we have a toal keyspace size of 11,110
If we consider that the encrypter uses an independent (other) key for the Polybius square creation, we would have to compute 26! ≈ 2^88.4 for the number of possible different Polybius squares. In this case, we have to compute for the “complex” Bazeries cipher 11,110 ∙ 2^88.4 which is about 2^101.8.
To compute the unicity distance (of the complex case), we have to divide the entropy of the keyspace with the redundancy of the language:
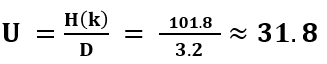
So we would need a ciphertext with a minimum length of 32 letters to obtain only one valid (and the correct) solution via cryptanalysis.
A YouTube Video about the Bazeries Cipher
I also created a YouTube vide about the Bazeries cipher: