I recently got some interesting feedback to the “Break reduced RSA” YouTube video I made some time ago. Of course I used CrypTool 2 (CT2) in that video. One viewer asked me, why we chose to generate non-safe primes, as well as if the quadratic sieve component of CT2 is able to break RSA challenge numbers. My answer to the second question: Since we have a quite old implementation of msieve (the library we use) converted to C# long ago, I don’t think the factorization algorithm is as powerful as the current state-of-the-art factorization libraries. Nevertheless, it is “good enough” to show how to break RSA (up to N in range of 2^300).
The answer to the safe prime question: Good question! I never thought of generating such numbers in CT2 and thought standard prime numbers are ok for CT2. I mean, it is a tool for education and not meant for any security purposes. Nevertheless, in real world applications you use large primes for RSA with additional requirements: They should be safe. So I updated the RSA KeyGenerator component to also allow the generation of safe primes. But are safe prime numbers still needed with RSA modules in the range of 2^2048 and above? For the current state-of-the-art of RSA factorization, you may have a look at https://en.wikipedia.org/wiki/RSA_Factoring_Challenge.
But what is a safe prime?
A number p is a prime number, if it is only divisible by itself and by 1. For example 13 is a prime number, or 17, or 23, … etc. A “safe prime” number p is a number, that is prime AND (p – 1) / 2 is also a prime number which we then call a Sophie Germain prime. An example for a safe prime is 23, because (23 – 1) / 2 = 11 is a Sophie Germain prime. Safe prime numbers are more resistant against some factorization methods, which could be used to factorize the RSA’s N (which is the product of two large primes p and q).
But are safe primes really needed for RSA?
I questioned that myself and found a paper by Rivest, who is the R in RSA. Already in 1999, Rivest stated that: “We find that for practical purposes using large “random” primes offers security equivalent to that obtained by using “strong” primes. Current requirements for “strong” primes do not make them any more secure than randomly chosen primes of the same size. Indeed, these requirements can lead a general audience to believe that if a prime is “strong” that it is secure and that if it isn’t “strong” then it must be “weak” and hence insecure. This simply is not true.” [1]
Rivest speaks about “strong” primes, not about safe primes. Strong primes have additional properties, from which “safe” primes fullfil one. But today, the usage of just “random” primes is good enough to keep RSA secure, since the primes are so large, that the properties for “strong” and “safe” are negligible. The “safe” property for primes was introduced to counter special factorization algorithms, like Pollard-Rho. But the modules we use today with RSA are too large to be factored with e.g. Pollard-Rho.
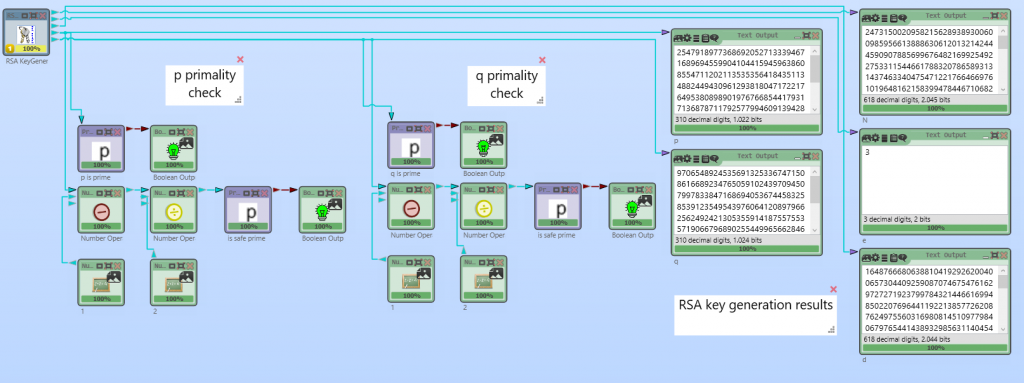
Nevertheless, now we have the choice in CT2 to generate either “random” or “safe” primes. Also, the RSA KeyGenerator uses a cryptographic random number generator during the generation of the RSA keys. In the CT2 workspace shown at the beginning of the blog article, we generate a 1024 bit RSA key and set the generator to “safe” prime generation. The prime test components evaluate the generated primes p and q and if both are “green” this means that the primes are safe.
You may be interested in my RSA YouTube video:
And you may also be interested in my “How to break reduced RSA” YouTube video:
[1] Rivest, Ronald L., and Robert D. Silverman. “Are Strong Primes Needed for RSA?” IN THE 1997 RSA LABORATORIES SEMINAR SERIES, SEMINARS PROCEEDINGS. 1999.
Nils
